File:TaniaPlot.png

Summary

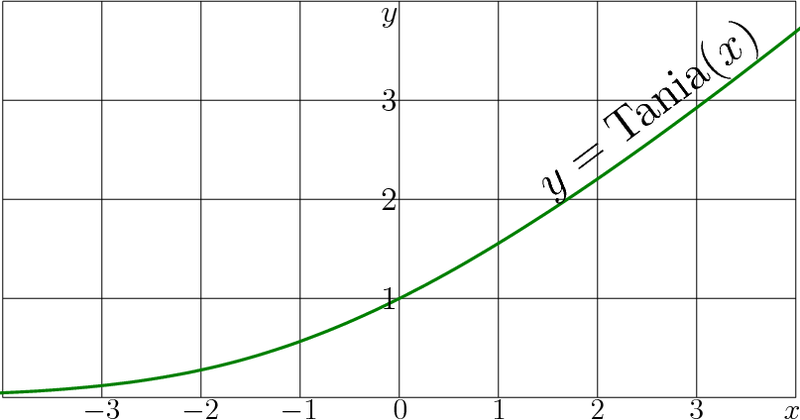
Title / Description	Explicit plot of the Tania function, ${\displaystyle y=\mathrm {Tania} (x)}$
Citizendium author & Copyright holder	Copyright © Dmitrii Kouznetsov. See below for licence/re-use information.
Date created	2011 September 22
Country of first publication	Japan
Notes	You can edit this page and add notes here which may be useful to people who wish to re-use this media.
Other versions	http://tori.ils.uec.ac.jp/TORI/index.php/File:TaniaPlot.png
Using this image on CZ	Please click here to add the credit line, then copy the code below to add this image to a Citizendium article, changing the size, alignment, and caption as necessary. {{Image|TaniaPlot.png|right|350px|Add image caption here.}}

Licensing

   

This media, TaniaPlot.png, is licenced under the Creative Commons Attribution 3.0 Unported License

You are free: To Share — To copy, distribute and transmit the work; To Remix — To adapt the work.
Under the following conditions: Attribution — You must attribute the work in the manner specified by the author or licensor (but not in any way that suggests that they endorse you or your use of the work).
For any reuse or distribution, you must make clear to others the licence terms of this work (the best way to do this is with a link to this licence's web page). Any of the above conditions can be waived if you get permission from the copyright holder. Nothing in this licence impairs or restricts the author's moral rights.
Read the full licence.

Source

C++ generator of the curve

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include <complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)

z_type ArcTania(z_type z) {return z + log(z) - 1. ;}

z_type ArcTaniap(z_type z) {return 1. + 1./z ;}

z_type TaniaTay(z_type z) { int n; z_type s;
s=1.+z*(.5+z*(1./16.+z*(-1./192.+z*(-1./3072.+z*(1.3/6144.+z*(-4.7/147456.
//+z*(7.3/4128768.) //some reserve term
)))))); DO(n,3) s+=(z-ArcTania(s))/ArcTaniap(s); return s ; }

z_type TaniaNega(z_type z){int n;z_type s=exp(z-exp(z)+1.);
DO(n,4) s+=(z-ArcTania(s))/ArcTaniap(s); return s ; }

z_type TaniaBig(z_type z){int n;z_type s=z; s=z-log(s)+1.;
DO(n,3) s+=(z-ArcTania(s))/ArcTaniap(s); return s ; }

z_type TaniaS(z_type z){int n; z_type s,t=z+z_type(2.,-M_PI);t*=2./9.; t=I*sqrt(t);
s=-1.+t*(3.+t*(-3.+t*(.75+t*(.3+t*(.9/16.+t*(-.3/7.+t*(-12.51/224. //+t*(-.9/28.)
)))))));
DO(n,3) s+=(z-ArcTania(s))/ArcTaniap(s); return s ; }

z_type Tania(z_type z){ z_type t;
if( fabs(Im(z))< M_PI && Re(z)<-2.51) return TaniaNega(z);
if( abs(z)>7. || Re(z)>3.8 ) return TaniaBig(z);
if( Im(z) > .7 ) return TaniaS(z);
if( Im(z) < -.7) return conj(TaniaS(conj(z)));
return TaniaTay(z);
}

void ado(FILE *O, int X, int Y)
{      fprintf(O,"%c!PS-Adobe-2.0 EPSF-2.0\n",'%');
       fprintf(O,"%c%cBoundingBox: 0 0 %d %d\n",'%','%',X,Y);
       fprintf(O,"/M {moveto} bind def\n");
       fprintf(O,"/L {lineto} bind def\n");
       fprintf(O,"/S {stroke} bind def\n");
       fprintf(O,"/s {show newpath} bind def\n");
       fprintf(O,"/C {closepath} bind def\n");
       fprintf(O,"/F {fill} bind def\n");
       fprintf(O,"/o {.1 0 360 arc C S} bind def\n");
       fprintf(O,"/times-Roman findfont 20 scalefont setfont\n");
       fprintf(O,"/W {setlinewidth} bind def\n");
       fprintf(O,"/RGB {setrgbcolor} bind def\n");}

#define M(x,y) fprintf(o,"%6.3f %6.3f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%6.3f %6.3f L\n",0.+x,0.+y);

main(){ int j,k,m,n; DB x,y, a;
FILE *o;o=fopen("taniaplot.eps","w");ado(o,808,408);
fprintf(o,"404 4 translate\n 100 100 scale\n");
for(m=-4;m<5;m++){ M(m,0)L(m,4)}
for(n=0;n<5;n++){ M(-4,n)L(4,n)}
fprintf(o,".01 W 0 0 0 RGB S\n");
// for(n=0;n<380;n++){y=.02+.01*n; x=ArcTania(y); if(n==0)M(x,y) else L(x,y) }
for(n=0;n<82;n++){ x=-4.03+.1*n; y=Re(Tania(x)); if(n==0)M(x,y) else L(x,y) }
fprintf(o,".03 W 0 .5 0 RGB S\n");
fprintf(o,"showpage\n%cTrailer",'%'); fclose(o);
      system("epstopdf taniaplot.eps");
      system(    "open taniaplot.pdf"); //these 2 commands may be specific for macintosh
getchar(); system("killall Preview");// if run at another operational sysetm, may need to modify
}

Latex generator of the lables

% Gerenator of TaniaPlot.png  

% Save the paragraph below as  TaniaPlot.tex  

% After the latexing and generation TaniaPlot.pdf  

%> convert TaniaPlot.pdf TaniaPlot.png  

% Copyleft 2011 by Dmitrii Kouznetsov  

\documentclass[12pt]{article} % 

\usepackage{geometry} % 

\usepackage{graphicx} % 

\usepackage{rotating} % 

\paperwidth 810pt % 

\paperheight 426pt % 

\topmargin -103pt % 

\oddsidemargin -96pt % 

\textwidth 1200pt % 
 
\textheight 600pt % 

\pagestyle {empty} % 

\newcommand \sx {\scalebox} % 

\newcommand \rot {\begin{rotate}} % 
 
\newcommand \ero {\end{rotate}} % 

\newcommand \ing {\includegraphics} % 

\begin{document} % 

\sx{1}{ \begin{picture}(808,410) % 

\put(1,9){\ing{taniaplot}} % 

\put(388,394){\sx{2.8}{$y$}} % 

\put(388,303){\sx{2.8}{$3$}} % 

\put(388,203){\sx{2.8}{$2$}} % 

\put(388,103){\sx{2.8}{$1$}} % 

\put( 86,-9){\sx{2.5}{$-3$}} % 

\put(186,-9){\sx{2.5}{$-2$}} % 

\put(286,-9){\sx{2.5}{$-1$}} % 

\put(400,-9){\sx{2.5}{$0$}} % 

\put(500,-9){\sx{2.5}{$1$}} % 

\put(600,-9){\sx{2.5}{$2$}} % 

\put(700,-9){\sx{2.5}{$3$}} % 

\put(796,-9){\sx{2.5}{$x$}} % 

\put(560,214){\rot{37}\sx{4}{$y=\mathrm{Tania}(x)$}\ero} % 

\end{picture} % 

} % 

\end{document}