Biot-Savart law

From Citizendium
Revision as of 06:00, 4 July 2008 by imported>Paul Wormer (→‎Laplace's formula)
Jump to navigation Jump to search
This article is developing and not approved.
 Main Article
 Discussion
Related Articles  [?]
Bibliography  [?]
External Links  [?]
Citable Version  [?]
 
https://en.citizendium.org/wiki/index.php?title=Biot-Savart_law&printable=yes
This editable Main Article is under development and subject to a disclaimer.

In physics, more particularly in electrodynamics, the law first formulated by Jean-Baptiste Biot and Félix Savart [1] describes the magnetic induction B (proportional to the magnetic field H) caused by a direct electric current in a wire. Biot and Savart interpreted their measurements by an integral relation. Laplace gave a differential form of their result, which now often is also referred to as the Biot-Savart law, or sometimes as the Biot-Savart-Laplace law. By integrating Laplace's equation over an infinitely long wire, the original integral form of Biot and Savart is obtained.

Ørsted's discovery

The Danish physicist Ørsted noticed in April 1820, while experimenting with the Voltaic pile, an effect of an electric current on a permanent magnet. He wrote a Latin publication which he sent round Europe. François Arago demonstrated the discovery at the French Académie des Sciences (11 September 1820), which inspired Jean-Baptiste Biot and André-Marie Ampère to investigate the effect further. At a meeting of the Académie des Sciences on 30 October 1820, Biot and Savart announced that the magnetic force exerted by a long conductor on a magnetic pole falls off with the reciprocal of the distance and is orientated perpendicular to the wire. Simultaneously they published this in a short note. Laplace generalized their result mathematically.

Laplace's formula

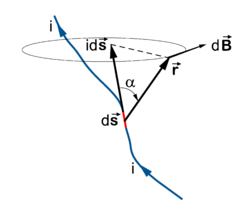
Magnetic induction dB at point r due to infinitesimal piece ds (red) of wire (blue) transporting electric current i.

The infinitesimal magnetic induction at point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \vec{\mathbf{r}} } (see figure on the right) is given by the following formula due to Laplace,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d\vec{\mathbf{B}} = k \frac{i d\vec{\mathbf{s}} \times \vec{\mathbf{r}}} {|\vec{\mathbf{r}}|^3}, }

where the magnetic induction is given as a vector product, i.e., is perpendicular to the plane spanned by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle d\vec{\mathbf{s}} } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \vec{\mathbf{r}} } . The electric current i is constant in time. The piece of the wire contributing to the magnetic induction can be seen as a vector of infinitesimal length ds and with direction tangent to the wire. The constant k depends on the units chosen. In rationalized SI units k is the magnetic constant (vacuum permeability) divided by 4π. The magnetic constant μ0 = 4π ×10−7 N/A2 (newton divided by ampere squared). In Gaussian units k = 1 / c (one over the velocity of light).

If we remember the fact that the vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \vec{\mathbf{r}}} has dimension length, we see that this equation is an Inverse-square law.

Infinite straight conductor

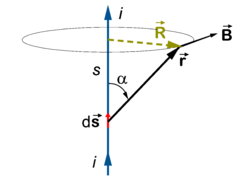
Field B due to current i in infinitely long straight wire.

Take a straight, infinitely long, conducting wire transporting the current i. Write, using R = r sinα (see the figure),

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d\vec{\mathbf{s}} \times \vec{\mathbf{r}} = \hat{\mathbf{e}} \,r\sin\alpha\, ds = \hat{\mathbf{e}}\, R\,ds, }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \hat{\mathbf{e}} } is a unit vector along Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \mathbf{B}} , which is perpendicular to the plane spanned by the wire and the vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \vec{\mathbf{R}}} perpendicular to the wire. Note that if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle d\vec{\mathbf{s}} } is moved along the wire, all contributions from the segments to the magnetic induction are along this unit vector. Hence, if we integrate over the wire we add up all these contributions, so that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\mathbf{B}} = \hat{\mathbf{e}} \,i R k \int_{-\infty}^{\infty} \frac{ds}{(s^2+R^2)^{3/2}} }

where, by the Pythagorean theorem,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{\mathbf{r}}|^2 = s^2 + R^2. }

Substitution of y = s / R and y = cotφ = cosφ / sinφ, successively, gives

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{\mathbf{B}}| = \frac{ik}{R} \int_{-\infty}^{\infty} \frac{dy}{(y^2+1)^{3/2}} = \frac{ik}{R} \int_{0}^{\pi} \sin\phi \, d\phi = \frac{2 ik}{R}, }

where i is the current and R the distance of the point of observation of the magnetic induction to the wire. The constant k depends on the choice of electromagnetic units and is μ0/4π = 10−7 henry/m [= Vs/A = N/A2] in rationalized SI units. In Gaussian units k = 1/c. This equation gives the original formulation of Biot and Savart. The SI dimension of B is T (tesla: 1 T = 1 N/(Am), newton divided by ampere meter). A field of 1 T (SI) corresponds to 10000 gauss (cgs units).

Historically, this is the case considered by Biot and Savart.

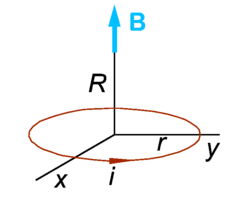
Magnetic field on axis of circular current

A current i runs on circle of radius r in x-y plane. At a distance R of the center there is a magnetic induction B along the z-axis.

The Biot-Savart expression can be integrated in cylinder coordinates for a point R on the z-axis. This gives (see figure on the right) a vector parallel to the z-axis of magnitude

Note that the direction of the electric current i and the magnetic induction B are related according to the right-hand screw rule: the screw is driven into the direction of B and rotated along i. The factor k is μ0/4π for SI units and 1/c for Gaussian units.

Generalized Biot-Savart-Laplace law

From hereon vectors are indicated by bold letters, arrows on top are omitted.

In the above we wrote i for the current, which is equal to the current density J times the cross section A of the wire. If the current density J is not constant over the cross section, i.e., J = J(r' ), we must use a surface integral over the cross section A. Rather than introducing a surface element, we multiply immediately by ds and obtain an infinitesimal volume element Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle d\mathbf{r}' \equiv dV} ,

Piece of wire of cross section A and length ds, volume d r' ≡ dV = Ads
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i d\mathbf{s} \rightarrow \iint_{A} \mathbf{J}(\mathbf{r}') d\mathbf{r}', }

where we defined the current density J as a vector parallel to the line segment ds and of magnitude J(r'). The volume element has height |ds| and base an infinitesimal surface element of the cross section A. The B-field at point r, due to a volume V = As of the current becomes,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{B}(\mathbf{r}) = k \iiint_{V} \frac{\mathbf{J}(\mathbf{r}') \times (\mathbf{r}-\mathbf{r'})} {|\mathbf{r}-\mathbf{r'}|^3}d\mathbf{r}' . }

Note that:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\mathbf{r}-\mathbf{r'}}{|\mathbf{r}-\mathbf{r'}|^3} = \boldsymbol{\nabla} \left( \frac{1}{|\mathbf{r}-\mathbf{r'}|} \right), }

where we choose the nabla operator, the gradient, to act on the unprimed coordinates and hence it may be moved outside the integral, giving the following generalized form of the Biot-Savart-Laplace law for the magnetic induction at point r:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{B}(\mathbf{r}) = k \boldsymbol{\nabla} \times \iiint_{V} \frac{\mathbf{J}(\mathbf{r}')} {|\mathbf{r}-\mathbf{r'}|}d\mathbf{r}', \qquad\qquad\qquad\qquad\qquad\qquad\qquad(1). }

Here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \boldsymbol{\nabla} \times } is the curl and V is a finite volume of the current generating the B-field. The total B-field is obtained by having V encompass all current (integrating over all current).

Consistency with Maxwell equations

The expression for B given in Eq. (1) is a solution of the Maxwell equations. This is of interest as it confirms the generally accepted notion that the Maxwell equations form a set of postulates for classical electrodynamics. All electrodynamic results, including Biot-Savart's law, must be derivable from them. We will show that the Biot-Savart-Laplace law can indeed be seen as a consequence of the Maxwell postulates, although Biot and Savart made their discovery some forty-five years before Maxwell.

Since it is known from vector analysis that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\nabla}\cdot\Big(\boldsymbol{\nabla}\times \mathbf{V}(\mathbf{r})\Big) = 0 }

for any vector field V(r), it is immediately clear that B in Eq. (1) satisfies the following Maxwell equation:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\nabla}\cdot\mathbf{B}(\mathbf{r}) = 0 . }

This equation states in fact that electric current cannot give a magnetic charge (magnetic monopole).

The one other Maxwell equation of interest is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\nabla}\times\mathbf{B}(\mathbf{r}) = 4\pi k \mathbf{J}(\mathbf{r}), \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad(2) }

where we assumed that there are no time-dependent electric fields present i.e., that displacement currents are zero. This equation was first formulated in integral form by Ampère, as was acknowledged by Maxwell. In SI units 4πk is equal to the vacuum permeability μ0. In the proof we will need the following mathematical results

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \boldsymbol{\nabla}\times( \boldsymbol{\nabla}\times \mathbf{V}) &= \boldsymbol{\nabla} (\boldsymbol{\nabla}\cdot\mathbf{V}) - \nabla^2 \mathbf{V} \\ \boldsymbol{\nabla} \frac{1}{|\mathbf{r}-\mathbf{r'}|} &= -\boldsymbol{\nabla}' \frac{1}{|\mathbf{r}-\mathbf{r'}|} \\ \nabla^2 \frac{1}{|\mathbf{r}-\mathbf{r'}|} &= - 4\pi \delta(\mathbf{r}-\mathbf{r'}) \\ \boldsymbol{\nabla} \cdot \mathbf{J} &= 0 .\\ \end{align} }

The first equation is well-known in vector analysis, the second follows by differentiating to the components of r and r' and equating. The third equation has a Dirac delta function on the right-hand side and follows from distribution theory. The last equation follows from charge density (ρ) conservation and the continuity equation,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial \rho}{\partial t} = 0 \quad \hbox{and}\quad \boldsymbol{\nabla} \cdot \mathbf{J}+\frac{\partial \rho}{\partial t} = 0, }

respectively. This continuity equation for electric charge can be derived from the Maxwell equations. Now, upon substitution of Eq. (1) into the left-hand side of Eq. (2), we obtain:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \boldsymbol{\nabla}\times \mathbf{B}(\mathbf{r}) &= k \boldsymbol{\nabla}\times \boldsymbol{\nabla} \times \iiint_{V} \frac{\mathbf{J}(\mathbf{r}')} {|\mathbf{r}-\mathbf{r'}|}d\mathbf{r}' \\ &= k \boldsymbol{\nabla}\iiint \mathbf{J}(\mathbf{r}')\cdot \boldsymbol{\nabla} \left( \frac{1} {|\mathbf{r}-\mathbf{r'}|}\right) d\mathbf{r}' - k \iiint \mathbf{J}(\mathbf{r}') \nabla^2 \left( \frac{1}{|\mathbf{r}-\mathbf{r'}|}\right) d\mathbf{r}' \\ &= k \boldsymbol{\nabla}\iiint \Big(\boldsymbol{\nabla}' \cdot \mathbf{J}(\mathbf{r}')\Big) \left( \frac{1} {|\mathbf{r}-\mathbf{r'}|}\right) d\mathbf{r}' + 4\pi k \iiint \mathbf{J}(\mathbf{r}') \delta(\mathbf{r}-\mathbf{r'}) d\mathbf{r}' . \\ \end{align} }

In the first term of the last step we replaced the unprimed nabla by a primed one (times minus) and then applied a turn-over rule with the primed nabla. This turn-over rule can be justified by partial integration and gives a minus sign, or, in other words, nabla is an anti-hermitian operator. Using that the divergence of the current density vanishes and the defining property of the delta function, we get finally

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\nabla}\times \mathbf{B}(\mathbf{r}) = 4\pi k \mathbf{J}(\mathbf{r}). }

This shows that B(r) of Eq. (1) (the generalized Biot-Savart-Laplace law) substituted into the left-hand side of the Maxwell equation (2) is equal to the right-hand side of this Maxwell equation and hence we conclude that Eq. (1) is a solution of Eq. (2).

See also

References

  1. ↑ J.-B. Biot and F. Savart, Note sur le Magnétisme de la pile de Volta, Annales Chim. Phys. vol. 15, pp. 222-223 (1820), free online version

Further reading:

  • J. D. Jackson, Classical Electrodynamics, 2nd edition, John Wiley, New York (1975).
Retrieved from "https://citizendium.org/wiki/index.php?title=Biot-Savart_law&oldid=402002"