Revision as of 07:16, 18 July 2009 by imported>Paul Wormer
In analytic geometry, a reflection is a linear operation σ on a vector space with σ2 = 1, i.e., σ is an involution. Reflecting twice an arbitrary vector brings back the original vector :

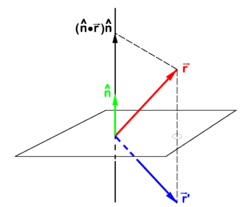
PD Image The vector

goes to

under reflection in a plane. The unit vector

is normal to mirror plane.
Reflection in a plane
If  is a unit vector normal (perpendicular) to a plane—the mirror plane—then
is a unit vector normal (perpendicular) to a plane—the mirror plane—then  is the projection of
is the projection of  on this unit vector. From the figure it is evident that
on this unit vector. From the figure it is evident that

If a non-unit normal  is used then substitution of
is used then substitution of

gives the mirror image,

This relation can be immediately generalized to m-dimensional inner product spaces. Let the space Vm allow an orthogonal direct sum decomposition into a 1-dimensional and a (m−1)-dimensional subspace,

and let v be an element of the one-dimensional space V1 then the involution

is a reflection of r in the hyperplane Vm−1. (By definition a hyperplane is an m−1-dimensional linear subspace of a linear space of dimension m.) The inner product of two vectors v and w is notated as (v, w), which is common for vector spaces of arbitrary dimension.













