< User:Aleksander StosRevision as of 07:06, 13 August 2007 by imported>Aleksander Stos
This is an experimental draft. For a brief description of the project and motivations click here.
Complex numbers are defined as ordered pairs of reals:

Such pairs can be added and multiplied as follows
- addition:

- multiplication:

 with the addition and the multiplication is the field of complex numbers.
with the addition and the multiplication is the field of complex numbers.
To perform basic computations it is convenient to introduce the imaginary unit, i=(0,1).[1] It has the property  Any complex number
Any complex number  can be written as
can be written as  (this is often called the algebraic form) and vice-versa. The numbers a and b are called the real part and the imaginary part of z, respectively. We denote
(this is often called the algebraic form) and vice-versa. The numbers a and b are called the real part and the imaginary part of z, respectively. We denote  and
and  Notice that i makes the multiplication quite natural:
Notice that i makes the multiplication quite natural:

The square root of number in the denominator in the above formula is called the modulus of z and denoted by  ,
,

We have for any two complex numbers  and
and 

 provided
provided 

For  we define also
we define also  , the conjugate, by
, the conjugate, by  Then we have
Then we have


 provided
provided 

Complex numbers may be naturally represented on the complex plane, i.e.  corresponds to the point (x,y), see the fig. 1.
corresponds to the point (x,y), see the fig. 1.
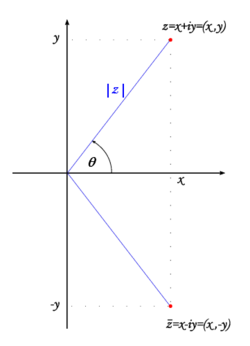
Fig. 1. Graphical representation of a complex number and its conjugate
- ↑ in some applications it is denoted by j as well.


























