Relative permeability: Difference between revisions
imported>John R. Brews (switch to relabeled figure) |
imported>John R. Brews (Grassmann) |
||
| Line 12: | Line 12: | ||
:<math>\mu_r = 1+\chi_m \ . \ \mathrm{SI\ units} \ . </math> | :<math>\mu_r = 1+\chi_m \ . \ \mathrm{SI\ units} \ . </math> | ||
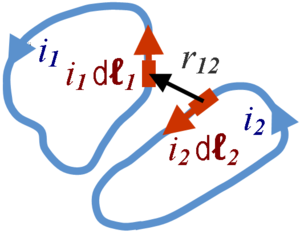
The [[Ampere's equation|Ampère force]] exerted between infinitesimal current elements from two loops carrying currents ''I<sub>i</sub>'' and ''I<sub>j</sub>'' and immersed in a magnetic medium with relative permeability ''μ<sub>r</sub>'' is changed by a factor ''μ<sub>r</sub>''. The infinitesimal current elements have vector components ''I<sub>i</sub>''d'''ℓ<sub>i</sub>''' and ''I<sub>j</sub>''d'''ℓ<sub>j</sub>''' where the incremental lengths are directed along the wire at the location of the element, and pointing in the direction of the current. | The [[Ampere's equation|Ampère force]] exerted between infinitesimal current elements from two loops carrying currents ''I<sub>i</sub>'' and ''I<sub>j</sub>'' and immersed in a magnetic medium with relative permeability ''μ<sub>r</sub>'' is changed by a factor ''μ<sub>r</sub>''. The infinitesimal current elements have vector components ''I<sub>i</sub>''d'''ℓ<sub>i</sub>''' and ''I<sub>j</sub>''d'''ℓ<sub>j</sub>''' where the incremental lengths are directed along the wire at the location of the element, and pointing in the direction of the current. Ampère's original force law is:<ref name=Assis> | ||
See for example, {{cite book |title=Weber's electrodynamics |author=André Koch Torres Assis |pages=p. 86 |url=http://books.google.com/books?id=SpUHp9P9pxsC&pg=PA86 |isbn=0792331370 |year=1994 |publisher=Springer}}, or {{cite book |title=Inductance and force calculations in electrical circuits |author=Marcelo de Almeida Bueno, André Koch Torres Assis |chapter=§5.1: Ampère's force |pages=pp. 51 ''ff'' |url=http://books.google.com/books?id=td7jh429VGsC&pg=PA52 |isbn=9781560729174 |year=2001 |publisher=Nova Science Publishers}} | See for example, {{cite book |title=Weber's electrodynamics |author=André Koch Torres Assis |pages=p. 86 |url=http://books.google.com/books?id=SpUHp9P9pxsC&pg=PA86 |isbn=0792331370 |year=1994 |publisher=Springer}}, or {{cite book |title=Inductance and force calculations in electrical circuits |author=Marcelo de Almeida Bueno, André Koch Torres Assis |chapter=§5.1: Ampère's force |pages=pp. 51 ''ff'' |url=http://books.google.com/books?id=td7jh429VGsC&pg=PA52 |isbn=9781560729174 |year=2001 |publisher=Nova Science Publishers}} | ||
| Line 20: | Line 20: | ||
:<math>d^2\mathbf{F_{ij}} = -d^2\mathbf{F_{ji}} = I_i I_j \frac{\mu_r \mu_0} {4\pi} \frac{\mathbf{\hat{u}_{ij}}}{r^2_{ij}}\left( 2\ (d \boldsymbol{\ell_i \cdot} d\boldsymbol{\ell_j})-3( \mathbf{ \hat{u}_{ij}\cdot } d\boldsymbol{ \ell_i} )(\mathbf{ \hat{u}_{ij} \cdot}d\boldsymbol{\ell_j})\right ) \ , </math> | :<math>d^2\mathbf{F_{ij}} = -d^2\mathbf{F_{ji}} = I_i I_j \frac{\mu_r \mu_0} {4\pi} \frac{\mathbf{\hat{u}_{ij}}}{r^2_{ij}}\left( 2\ (d \boldsymbol{\ell_i \cdot} d\boldsymbol{\ell_j})-3( \mathbf{ \hat{u}_{ij}\cdot } d\boldsymbol{ \ell_i} )(\mathbf{ \hat{u}_{ij} \cdot}d\boldsymbol{\ell_j})\right ) \ , </math> | ||
with '''û<sub>ij</sub>''' a unit vector pointing along the line joining element ''j'' to element ''i'' and ''r<sub>ij</sub>'' the length of this line. The force element is second order because it is a product of two infinitesimals. | with '''û<sub>ij</sub>''' a unit vector pointing along the line joining element ''j'' to element ''i'' and ''r<sub>ij</sub>'' the length of this line. The force element is second order because it is a product of two infinitesimals. This force law leads to the same force between closed current loops as the more commonly used Grassmann's law: | ||
:<math>d^2\mathbf{F_{ij}} = I_i I_j \frac{\mu_r \mu_0} {4\pi} \frac{1}{r^2_{ij}}\left( \ (d \boldsymbol{\ell_i \cdot} d\boldsymbol{\ell_j})\mathbf{\hat{u}_{ij}}-( \mathbf{ \hat{u}_{ij}\cdot } d\boldsymbol{ \ell_i} )d\boldsymbol{\ell_j})\right ) \ , </math> | |||
which is not obviously symmetric under exchange of the indices ''i'' and ''j'', but is readily derived from the [[Biot-Savart law]], and is the preferred expression for the force. | |||
Empirically it is observed that the force may increase or decreases due to the presence of the magnetic medium, hence the relative permittivity μ<sub>r</sub> may be greater than or less than 1. For simple media, if μ<sub>r</sub> < 1, the medium is termed ''diamagnetic''; if > 1 ''paramagnetic''. Only [[classical vacuum]] has μ<sub>r</sub> = 1 (exact). A typical diamagnetic susceptibility is about −10<sup>−5</sup>, while a typical paramagnetic susceptibility is about 10<sup>−4</sup>. It should be noted that the use of a constant as the relative permeability of a substance is an approximation, even for [[Vacuum (quantum electrodynamic)|quantum vacuum]]. A more complete representation recognizes that all media exhibit departures from this approximation, in particular, a dependence on field strength, a dependence upon the rate of variation of the field in both time and space, and a dependence upon the direction of the field. In many materials these dependencies are slight; in others, like [[Ferromagnetism|ferromagnets]], they are pronounced. | Empirically it is observed that the force may increase or decreases due to the presence of the magnetic medium, hence the relative permittivity μ<sub>r</sub> may be greater than or less than 1. For simple media, if μ<sub>r</sub> < 1, the medium is termed ''diamagnetic''; if > 1 ''paramagnetic''. Only [[classical vacuum]] has μ<sub>r</sub> = 1 (exact). A typical diamagnetic susceptibility is about −10<sup>−5</sup>, while a typical paramagnetic susceptibility is about 10<sup>−4</sup>. It should be noted that the use of a constant as the relative permeability of a substance is an approximation, even for [[Vacuum (quantum electrodynamic)|quantum vacuum]]. A more complete representation recognizes that all media exhibit departures from this approximation, in particular, a dependence on field strength, a dependence upon the rate of variation of the field in both time and space, and a dependence upon the direction of the field. In many materials these dependencies are slight; in others, like [[Ferromagnetism|ferromagnets]], they are pronounced. | ||
Revision as of 11:04, 18 April 2011
In physics, in particular in magnetostatics, the relative permeability is an intrinsic property of a magnetic material. It is usually denoted by μr. For simple magnetic materials, using SI units, μr is related to the proportionality constant between the magnetic flux density B and the magnetic field H, namely B = μr μ0 H, where μ0 is the magnetic constant. The relative permeability describes the ease by which a magnetic medium may be magnetized.
A related quantity is the magnetic susceptibility, denoted by χm, related to the magnetic permeability in SI units by:[1]
The Ampère force exerted between infinitesimal current elements from two loops carrying currents Ii and Ij and immersed in a magnetic medium with relative permeability μr is changed by a factor μr. The infinitesimal current elements have vector components Iidℓi and Ijdℓj where the incremental lengths are directed along the wire at the location of the element, and pointing in the direction of the current. Ampère's original force law is:[2]
with ûij a unit vector pointing along the line joining element j to element i and rij the length of this line. The force element is second order because it is a product of two infinitesimals. This force law leads to the same force between closed current loops as the more commonly used Grassmann's law:
which is not obviously symmetric under exchange of the indices i and j, but is readily derived from the Biot-Savart law, and is the preferred expression for the force.
Empirically it is observed that the force may increase or decreases due to the presence of the magnetic medium, hence the relative permittivity μr may be greater than or less than 1. For simple media, if μr < 1, the medium is termed diamagnetic; if > 1 paramagnetic. Only classical vacuum has μr = 1 (exact). A typical diamagnetic susceptibility is about −10−5, while a typical paramagnetic susceptibility is about 10−4. It should be noted that the use of a constant as the relative permeability of a substance is an approximation, even for quantum vacuum. A more complete representation recognizes that all media exhibit departures from this approximation, in particular, a dependence on field strength, a dependence upon the rate of variation of the field in both time and space, and a dependence upon the direction of the field. In many materials these dependencies are slight; in others, like ferromagnets, they are pronounced.
Notes
- ↑ For example see Yehuda Benzion Band. Light and matter: electromagnetism, optics, spectroscopy and lasers. John Wiley and Sons, p. 242. ISBN 0471899313.
- ↑ See for example, André Koch Torres Assis (1994). Weber's electrodynamics. Springer, p. 86. ISBN 0792331370. , or Marcelo de Almeida Bueno, André Koch Torres Assis (2001). “§5.1: Ampère's force”, Inductance and force calculations in electrical circuits. Nova Science Publishers, pp. 51 ff. ISBN 9781560729174.