Electric dipole

In chemistry, an electric dipole is a charge distribution consisting of two electric point charges of opposite sign and equal magnitude.

Often the requirement is added to the definition that the distance r between the two point charges must be "small"—one then speaks of a point dipole. Small is a relative concept and requires further specification. In general one is interested in the electric potential field due to the dipolar charge distribution at a distance R from the midpoint of the dipole. If it holds that r << R then, seen from the distance R, the dipolar charge distribution is a point dipole.

In physics, one meets the following related, but different, definition: a dipole of an electrostatic charge distribution ρ(r) is its first moment,

${\boldsymbol {\mu }}\;{\stackrel {\mathrm {def} }{=}}\;\int \,\mathbf {r} \,\rho (\mathbf {r} )\,\mathrm {d} \mathbf {r}$

In this definition a dipole is a vector depending on the characteristics of the charge distribution.

Combining the two definitions, one considers two point charges: q₁ at position r₁ and q₂ at position r₂. The charge distribution is written in terms of Dirac delta functions

$\rho (\mathbf {r} )=q_{1}\delta (\mathbf {r} -\mathbf {r} _{1})+q_{2}\delta (\mathbf {r} -\mathbf {r} _{2}),$

where the charges are of opposite sign and equal magnitude. The first moment of this charge distribution is

${\boldsymbol {\mu }}=\int \,\mathbf {r} \,\rho (\mathbf {r} )\,\mathrm {d} \mathbf {r} =\int \,\mathbf {r} \,{\big [}q_{1}\delta (\mathbf {r} -\mathbf {r} _{1})+q_{2}\delta (\mathbf {r} -\mathbf {r} _{2}){\big ]}\,\mathrm {d} \mathbf {r} =q_{1}\mathbf {r} _{1}+q_{2}\mathbf {r} _{2}=|q|\,(\mathbf {r} _{2}-\mathbf {r} _{1}),$

where we used q₁ = −|q| and q₂ = |q|.

This leads to a third possible definition: a dipole is a vector pointing from a negative electric point charge to a positive electric point charge, where both charges are of the same magnitude. The size (length) of the dipole is the distance between the point charges times the magnitude of the charges.

In chemistry dipole moments of molecules are often quoted to indicate charge separations in molecules. Usually chemists are only interested in absolute values, a large dipole indicates a highly polar molecule (much separation of charge), whereas non-polar molecules have negligible dipoles. In the rare case that the sign of a dipole plays a role, most (organic) chemists use a convention that is opposite to the convention just discussed: they let the dipole point from a positively charged region in the molecule to a negatively charged region.

Field of point dipole

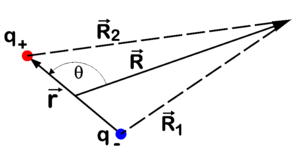
The potential field of a point dipole μ at a point R (a vector pointing from the dipole to an arbitrary in space, see the figure) is given by

$V_{\mathrm {dip} }(\mathbf {R} )={\frac {{\boldsymbol {\mu }}\cdot \mathbf {R} }{4\pi \epsilon _{0}\,R^{3}}}$

where R is the length of R, the dot indicates the dot product between μ and R, and ε₀ is the electric constant (vacuum permittivity).

Proof

The potential field of a point dipole can be determined fairly easily, see the figure for the symbols. In the equations we indicate vectors with bold letters, not with arrows on top as in the figure. The length of a vector is indicated with the corresponding symbol in italics. Write

${\begin{aligned}\mathbf {R} _{1}&=\mathbf {R} +{\frac {1}{2}}\mathbf {r} &\Longrightarrow &|\mathbf {R} _{1}|^{2}={\Big (}\mathbf {R} +{\frac {1}{2}}\mathbf {r} {\Big )}\cdot {\Big (}\mathbf {R} +{\frac {1}{2}}\mathbf {r} {\Big )}=R^{2}\left[1+{\Big (}{\frac {r}{2R}}{\Big )}^{2}+{\frac {r}{R}}\cos \theta \right]\\\mathbf {R} _{2}&=\mathbf {R} -{\frac {1}{2}}\mathbf {r} &\Longrightarrow &|\mathbf {R} _{1}|^{2}={\Big (}\mathbf {R} -{\frac {1}{2}}\mathbf {r} {\Big )}\cdot {\Big (}\mathbf {R} -{\frac {1}{2}}\mathbf {r} {\Big )}=R^{2}\left[1+{\Big (}{\frac {r}{2R}}{\Big )}^{2}-{\frac {r}{R}}\cos \theta \right]\\\end{aligned}}$

PD Image
Field of two point charges

Use the expansions, valid for x << 1,

${\frac {1}{\sqrt {1\mp x}}}=1\pm {\frac {1}{2}}x.$

Since r << R it follows that r/R << 1 and hence

${\begin{aligned}{\frac {1}{|\mathbf {R} _{1}|}}&\approx {\frac {1}{R}}{\big (}1-{\frac {r}{2R}}\cos \theta {\big )}\\{\frac {1}{|\mathbf {R} _{2}|}}&\approx {\frac {1}{R}}{\big (}1+{\frac {r}{2R}}\cos \theta {\big )}\\\end{aligned}}$

The Coulomb potential at the point R is the sum of the potentials due to the two charges, which are of equal magnitude q and of opposite sign,

${\begin{aligned}V(\mathbf {R} )\equiv &{\frac {q_{-}}{4\pi \epsilon _{0}\,|\mathbf {R} _{1}|}}+{\frac {q_{+}}{4\pi \epsilon _{0}\,|\mathbf {R} _{2}|}}\\\approx &{\frac {q}{4\pi \epsilon _{0}\,R}}\left[-1+{\frac {r}{2R}}\cos \theta +1+{\frac {r}{2R}}\cos \theta \right]={\frac {q\;\mathbf {r} \cdot \mathbf {R} }{4\pi \epsilon _{0}\,R^{3}}}={\frac {{\boldsymbol {\mu }}\cdot \mathbf {R} }{4\pi \epsilon _{0}\,R^{3}}}\end{aligned}}$

where we used

${\frac {r\cos \theta }{R^{2}}}={\frac {rR\cos \theta }{R^{3}}}={\frac {\mathbf {r} \cdot \mathbf {R} }{R^{3}}}\quad {\hbox{and}}\quad {\boldsymbol {\mu }}\equiv q\mathbf {r} .$