User talk:Paul Wormer/scratchbook: Difference between revisions
imported>Paul Wormer |
imported>Paul Wormer No edit summary |
||
| Line 1: | Line 1: | ||
The '''second law of thermodynamics''', as formulated in the middle of the 19th century by [[William Thomson]] (Lord Kelvin) and [[Rudolf Clausius]], states that it is impossible to gain mechanical energy from heat flowing from a ''cold'' to a ''hot'' body. Clausius postulated that the opposite is the case | The '''second law of thermodynamics''', as formulated in the middle of the 19th century by [[William Thomson]] (Lord Kelvin) and [[Rudolf Clausius]], states that it is impossible to gain mechanical energy (work) from heat flowing from a ''cold'' to a ''hot'' body. Clausius postulated that the opposite is the case: it requires input of mechanical (or electric) energy to transport heat from a low- to a high-temperature object. In modern terms: a [[heat pump]], an [[air conditioner]], and a [[refrigerator]], devices that move heat from a cold to a warm place, cost energy. | ||
Thomson formulated the | Thomson formulated the second law in a slightly different, but equivalent way. He stated that it is impossible in a cyclic process to extract work from a single source of heat. In a cyclic process the heat source ends up in a thermodynamic state that is the same as in the beginning of the process; the heat source does not lose any net [[internal energy]]. In order that a cyclic process is in agreement with the [[first law of thermodynamics]] (i.e., conserves energy), it is necessary that the heat generated by the work is returned to the heat source. | ||
If the second law would not rule physics, there would be no energy shortage. For example, it would be possible—as already pointed out by Lord Kelvin—to propel ships by energy extracted from sea water. After all, the oceans contain immense amounts of internal energy. When one could extract just a small portion of it—whereby a slight cooling of the sea water would occur—and use this to propel a ship (a form of work), then ships could move without any net consumption of energy. It would ''not'' violate the [[first law of thermodynamics]], because the rotation of the ship's propellers would again heat the water and in total the energy of the supersystem "ship-plus-ocean" would be conserved, in agreement with the first law. Unfortunately, it is not possible, no work can be extracted from the water because it would be a single source of heat. Clausius would explain it by observing that ships are warmer than sea water (or at least they are not colder) and hence it needs work to transport heat from the sea to the ship. | |||
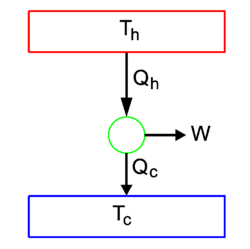
{{Image|Second law.png|right|250px| | {{Image|Second law.png|right|250px|Second law: If ''W'' > 0 then ''T''<sub>1</sub> > ''T''<sub>2</sub> and ''Q''<sub>out</sub> ≠ 0.}} | ||
One could conceive a similar setup on land where energy, extracted from the earth, would charge batteries, and heat, dissipated by electric currents generated by the batteries, would be given back to the earth. Unfortunately, this is also out of the question because of the same fundamental second law of thermodynamics. | |||
The second law is summarized in figure | The second law is summarized in the figure Two heat reservoirs are shown, one of absolute [[temperature]] ''T''<sub>1</sub> and the other of temperature ''T''<sub>2</sub>, ''T''<sub>1</sub> >''T''<sub>2</sub>. The reservoirs are coupled by a [[heat engine]] (green circle), a construct that converts heat ''Q''<sub>in</sub> into work ''W''. The "rest heat" ''Q''<sub>out</sub> is delivered to reservoir 2. The scheme of the figure invented by [[Sadi Carnot]], is an idealized representation of power-generating machines like [[steam engine]]s considered by Carnot himself. But the scheme applies also to an [[automobile]], a vehicle with an internal [[combustion engine]]. The high-temperature heat bath is formed by the cylinders which are hot because of the combustion of gasoline. The cold heat bath is formed by the environment of the car—the rest heat is delivered to the surroundings through the car's radiator. The cyclically moving pistons, that perform the actual work, form the heat engine. | ||
When net work ''W'' is performed by the engine on the surroundings (''W'' is positive and outgoing in the figure), the Kelvin principle states that ''Q''<sub>out</sub> ≠ 0, because otherwise there would be a single heat source. The Clausius principle states that for ''W'' > 0 it is necessary that ''T''<sub>1</sub> is larger than ''T''<sub>2</sub>. Hence, the second law states that it is not possible to convert all the heat ''Q''<sub>in</sub> delivered by the first reservoir into work, part of it becomes non-zero ''rest heat'' ''Q''<sub>out</sub> absorbed by the low temperature reservoir. In the case of a car it means that only part of the combustion energy delivered by the gasoline is converted into work, and that a running car by necessity heats up its environment by its rest heat. | |||
It can be shown that the efficiency η ≡ ''W'' / ''Q''<sub>in</sub> has a maximum: | |||
It can be | |||
:<math> | :<math> | ||
\eta \le \frac{T_1-T_2}{T_1}. | \eta \le \frac{T_1-T_2}{T_1}. | ||
</math> | </math> | ||
Thus, when the car cylinders operate at 500 °C ≈ 800 K and the environment is about 300 K, then | Thus, when the car cylinders operate at 500 °C ≈ 800 K and the environment is about 300 K, then | ||
η ≤ 500/800 = 62%. <ref>In reality most cars run at an efficiency of about 25%, far from the thermodynamic limit.</ref> It is important to note that this efficiency is a consequence of the second law of thermodynamics, and can only be raised by higher ''T''<sub>1</sub> not by a better streamline or other design improvements. | η ≤ 500/800 = 62%. <ref>In reality most cars run at an efficiency of about 25%, far from the thermodynamic limit.</ref> It is important to note that this limit to the efficiency is a consequence of the second law of thermodynamics, and can only be raised by higher ''T''<sub>1</sub> not by a better streamline of the car or other design improvements. | ||
==Mathematical expression of the second law== | ==Mathematical expression of the second law== | ||
We consider a single thermodynamic system of absolute temperature ''T'', and let ''DQ'' be a small amount of heat entering or leaving this system in a reversible (quasistatic) manner. In the article [[entropy]] it is proved from the Clausius/Kelvin principle that a thermodynamic system is characterized, not only its usual parameters as volume, pressure, etc., but also by the state variable ''S'', the entropy of the system. The differential ''dS'' is defined by | |||
:<math> | :<math> | ||
dS \;\stackrel{\mathrm{def}}{=}\; \frac{DQ}{T} | dS \;\stackrel{\mathrm{def}}{=}\; \frac{DQ}{T}. | ||
</math> | </math> | ||
The fact that ''S'' is a state function implies that the following holds for a ''reversible'' cyclic process, where the suffix "rev" is added to stress that this law holds only for reversible processes, | |||
:<math> | :<math> | ||
\oint \frac{DQ_\mathrm{rev}}{T} \equiv {\int\limits_1\limits^2}_{{\!\!}^{(I)}}\frac{DQ_\mathrm{rev}}{T} + {\int\limits_2\limits^1}_{{\!\!}^{(II)}} \frac{DQ_\mathrm{rev}}{T} = \oint dS_\mathrm{rev} = 0 . | \oint \frac{DQ_\mathrm{rev}}{T} \equiv {\int\limits_1\limits^2}_{{\!\!}^{(I)}}\frac{DQ_\mathrm{rev}}{T} + {\int\limits_2\limits^1}_{{\!\!}^{(II)}} \frac{DQ_\mathrm{rev}}{T} = \oint dS_\mathrm{rev} = 0 . | ||
| Line 31: | Line 29: | ||
This equation is the mathematical expression of the second law of thermodynamics for the special case of reversible processes. The cycle consists of two different paths in state space, denoted by I and II. The path integrals start and end at common points in state space, indicated by 1 and 2. | This equation is the mathematical expression of the second law of thermodynamics for the special case of reversible processes. The cycle consists of two different paths in state space, denoted by I and II. The path integrals start and end at common points in state space, indicated by 1 and 2. | ||
In order to show that conversely this equation yields the Clausius principle, we consider the heat engine in the figure as our system and assume that both heat baths are so large (or the engine so small) that one full cycle of the cycle does not change the temperatures of the baths. Then | |||
In order to show that conversely this equation yields the Clausius principle, we consider | |||
:<math> | :<math> | ||
\oint dS = \oint \frac{DQ_\mathrm{in}}{T_1} - \oint \frac{DQ_\mathrm{out}}{T_2} = | \oint dS = \oint \frac{DQ_\mathrm{in}}{T_1} - \oint \frac{DQ_\mathrm{out}}{T_2} = | ||
| Line 38: | Line 35: | ||
\Longrightarrow \frac{Q_\mathrm{in}}{Q_\mathrm{out}} = \frac{T_1}{T_2}, | \Longrightarrow \frac{Q_\mathrm{in}}{Q_\mathrm{out}} = \frac{T_1}{T_2}, | ||
</math> | </math> | ||
where we defined | where we defined | ||
:<math> | :<math> | ||
\oint \frac{DQ_\mathrm{in}}{T_1} = \frac{1}{T_1} \oint DQ_\mathrm{in} \equiv \frac{Q_\mathrm{in}}{T_1} | \oint \frac{DQ_\mathrm{in}}{T_1} = \frac{1}{T_1} \oint DQ_\mathrm{in} \equiv \frac{Q_\mathrm{in}}{T_1} | ||
</math> | </math> | ||
and likewise ''Q''<sub>out</sub>. The first law applied after a full cycle of the heat engine | and likewise ''Q''<sub>out</sub>. | ||
<!-- | |||
The first law applied after a full cycle of the heat engine | |||
:<math> | :<math> | ||
Q_\mathrm{in} = W + Q_\mathrm{out}, | Q_\mathrm{in} = W + Q_\mathrm{out}, | ||
Revision as of 05:17, 31 October 2009
The second law of thermodynamics, as formulated in the middle of the 19th century by William Thomson (Lord Kelvin) and Rudolf Clausius, states that it is impossible to gain mechanical energy (work) from heat flowing from a cold to a hot body. Clausius postulated that the opposite is the case: it requires input of mechanical (or electric) energy to transport heat from a low- to a high-temperature object. In modern terms: a heat pump, an air conditioner, and a refrigerator, devices that move heat from a cold to a warm place, cost energy.
Thomson formulated the second law in a slightly different, but equivalent way. He stated that it is impossible in a cyclic process to extract work from a single source of heat. In a cyclic process the heat source ends up in a thermodynamic state that is the same as in the beginning of the process; the heat source does not lose any net internal energy. In order that a cyclic process is in agreement with the first law of thermodynamics (i.e., conserves energy), it is necessary that the heat generated by the work is returned to the heat source.
If the second law would not rule physics, there would be no energy shortage. For example, it would be possible—as already pointed out by Lord Kelvin—to propel ships by energy extracted from sea water. After all, the oceans contain immense amounts of internal energy. When one could extract just a small portion of it—whereby a slight cooling of the sea water would occur—and use this to propel a ship (a form of work), then ships could move without any net consumption of energy. It would not violate the first law of thermodynamics, because the rotation of the ship's propellers would again heat the water and in total the energy of the supersystem "ship-plus-ocean" would be conserved, in agreement with the first law. Unfortunately, it is not possible, no work can be extracted from the water because it would be a single source of heat. Clausius would explain it by observing that ships are warmer than sea water (or at least they are not colder) and hence it needs work to transport heat from the sea to the ship.
One could conceive a similar setup on land where energy, extracted from the earth, would charge batteries, and heat, dissipated by electric currents generated by the batteries, would be given back to the earth. Unfortunately, this is also out of the question because of the same fundamental second law of thermodynamics.
The second law is summarized in the figure Two heat reservoirs are shown, one of absolute temperature T1 and the other of temperature T2, T1 >T2. The reservoirs are coupled by a heat engine (green circle), a construct that converts heat Qin into work W. The "rest heat" Qout is delivered to reservoir 2. The scheme of the figure invented by Sadi Carnot, is an idealized representation of power-generating machines like steam engines considered by Carnot himself. But the scheme applies also to an automobile, a vehicle with an internal combustion engine. The high-temperature heat bath is formed by the cylinders which are hot because of the combustion of gasoline. The cold heat bath is formed by the environment of the car—the rest heat is delivered to the surroundings through the car's radiator. The cyclically moving pistons, that perform the actual work, form the heat engine.
When net work W is performed by the engine on the surroundings (W is positive and outgoing in the figure), the Kelvin principle states that Qout ≠ 0, because otherwise there would be a single heat source. The Clausius principle states that for W > 0 it is necessary that T1 is larger than T2. Hence, the second law states that it is not possible to convert all the heat Qin delivered by the first reservoir into work, part of it becomes non-zero rest heat Qout absorbed by the low temperature reservoir. In the case of a car it means that only part of the combustion energy delivered by the gasoline is converted into work, and that a running car by necessity heats up its environment by its rest heat.
It can be shown that the efficiency η ≡ W / Qin has a maximum:
Thus, when the car cylinders operate at 500 °C ≈ 800 K and the environment is about 300 K, then η ≤ 500/800 = 62%. [1] It is important to note that this limit to the efficiency is a consequence of the second law of thermodynamics, and can only be raised by higher T1 not by a better streamline of the car or other design improvements.
Mathematical expression of the second law
We consider a single thermodynamic system of absolute temperature T, and let DQ be a small amount of heat entering or leaving this system in a reversible (quasistatic) manner. In the article entropy it is proved from the Clausius/Kelvin principle that a thermodynamic system is characterized, not only its usual parameters as volume, pressure, etc., but also by the state variable S, the entropy of the system. The differential dS is defined by
The fact that S is a state function implies that the following holds for a reversible cyclic process, where the suffix "rev" is added to stress that this law holds only for reversible processes,
This equation is the mathematical expression of the second law of thermodynamics for the special case of reversible processes. The cycle consists of two different paths in state space, denoted by I and II. The path integrals start and end at common points in state space, indicated by 1 and 2.
In order to show that conversely this equation yields the Clausius principle, we consider the heat engine in the figure as our system and assume that both heat baths are so large (or the engine so small) that one full cycle of the cycle does not change the temperatures of the baths. Then
where we defined
and likewise Qout.
Many, in fact most, thermodynamic processes are spontaneous and irreversible. A well-known spontaneous process is the flow of heat from a hot to a cold body. The opposite process—the transport of heat from a cold to a hot body—needs work (by the Clausius principle), the process is not spontaneous and accordingly not the reverse of the spontaneous flow of heat from hot to cold bodies. Another example of an irreversible process is Count Rumford's seminal cannon boring experiment where work is converted by friction into heat. It is impossible to revert this process, which is intuitively clear, but also contradicts the Kelvin principle, the impossibility of obtaining work from a single source of heat. The Joule-Thomson effect is yet another example of an irreversible process.
References
C. S. Helrich, Modern Thermodynamics with Statistical Mechanics, Springer (2009). Google books
- ↑ In reality most cars run at an efficiency of about 25%, far from the thermodynamic limit.