Complex number

Complex numbers are numbers of the form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a+bi} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} are real numbers and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} denotes a number satisfying Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^2=-1} . Of course, since the square of any real number is nonnegative, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} cannot be a real number. At first glance, it is not even clear whether such an object exists and can be reasonably called a number; for example, can we sensibly associate with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} natural operations such as addition and multiplication? As it happens, we can define mathematical operations for these "complex numbers" in a consistent and sensible way and, perhaps more importantly, using complex numbers provides mathematicians, physicists, and engineers with an extremely powerful approach to expressing parts of these sciences in a convenient and natural-feeling way.

Historical example

The need for complex numbers might have appeared for the first time during the sixteenth century, when Italian mathematicians like Scipione del Ferro, Niccolò Fontana Tartaglia, Gerolamo Cardano and Rafael Bombelli tried to solve cubic equations. Even for equations with three real solutions, the method they used sometimes required calculations with numbers whose squares are negative. Here is such an example (with modern notation). Let us consider the equation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^3=15x+4. \ }

Cardano's method for solving it suggests looking for a solution by writing it as a sum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=u+v} , where another condition on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} is to be decided later. Recording this in the equation, we have, once the left member is expanded,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u^3+3u^2v+3uv^2+v^3=15(u+v)+4, \ }

which can be written as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u^3+(3uv-15)(u+v)+v^3=4. \ }

Now we recall that we did not completely specify Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} ; we only required that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=u+v} . Hence, we can choose another condition on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} and $v$. We pick this condition to be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3uv-15=0} , or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle uv=5} , in order to simplify the above equation. This implies that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u^3} and $v^{3}$ are numbers whose sum and product are given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} u^3v^3=125, \\ u^3+v^3=4. \end{cases}}

It follows from the second equation that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v^3 = 4 - u^3} . Substituting this in the first equation, we get Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u^3 (4-u^3) = 125} . Hence we may find some values for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u^3} by solving the equation $y(4-y)=125$. Getting rid of the brackets and moving the number 125 to the left-hand side gives us the quadratic equation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y^2-4y+125=0. \ }

Its discriminant is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle\Delta=(-4)^2-4\cdot 125=-484=-22^2} , which is negative, so that the quadratic equation has no real solution: the usual formulae giving the solutions require taking the square root of the discriminant, which is undefined here.

Well, let us be bold and write Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle\Delta=\left(22\sqrt{-1}\right)^2} . Here, the symbol $\scriptstyle {\sqrt {-1}}$ denotes an hypothetical number whose square would be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1.} At this stage, such a number has no meaning (squares of real numbers are always nonnegative), but we use it in a purely formal way. Using this symbol, we can write the "solutions" to the quadratic equation as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u^3=\frac{4+22\sqrt{-1}}{2}=2+11\sqrt{-1} \mbox{ and }v^3=\frac{4-22\sqrt{-1}}{2}=2-11\sqrt{-1}.}

It remains to find cube roots of these "numbers". A straightforward calculation shows that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle u=2+\sqrt{-1}} and $\scriptstyle v=2-{\sqrt {-1}}$ do the job. For instance, remembering the rule Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle\left(\sqrt{-1}\right)^2=-1} , we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(2+\sqrt{-1}\right)^3=2^3+3\cdot 2^2\sqrt{-1}+3\cdot 2\left(\sqrt{-1}\right)^2+\left(\sqrt{-1}\right)^3}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =8+12\sqrt{-1}-6-\sqrt{-1}=2+11\sqrt{-1}.}

But now, going back to the original cubic equation, we get the real solution $\scriptstyle x=u+v=(2+{\sqrt {-1}})+(2-{\sqrt {-1}})=4$. One can verify it is indeed a solution, as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle 4^3=64=15\cdot 4+4} . And once this solution is found, it is easy to find the two other solutions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle -2\pm\sqrt3} , which are also real.

The fact that the formal calculations managed to give a real solution suggests that the "number" Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle\sqrt{-1}} may have some sense. But to really give it a legitimate status, one has to construct a new set of numbers, containing the real numbers, but also other numbers whose squares may be negative real numbers. This will be the set of complex numbers. A rigorous construction of this set as pairs of real numbers was given much later by William Rowan Hamilton in 1837; this construction is explained later in this article.

Working with complex numbers

As a first step in giving some legitimacy to the "number" $\scriptstyle {\sqrt {-1}}$, we will explain how to compute with it. How do you add, multiply and divide expressions with this number? It turns out that this is not that difficult; the main rule to keep in mind is that the square of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \sqrt{-1}} equals Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle -1} .

In the remainder of the article, we will use the letter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} to denote one solution of the equation $i^{2}=-1$, where we previously used Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \sqrt{-1}} . With this convention, all complex numbers can be written as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a + bi} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} are real numbers. We call Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} the real part of the complex number and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} the imaginary part. The complex number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a + 0i} whose imaginary part is zero is considered to be the same thing as the real number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} .

Basic operations

Addition of complex numbers is straightforward, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a + bi) + (c + di) = (a + c) + (b + d)i.} The result is again a complex number.

Multiplication is more interesting. Suppose we want to compute Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a+bi)(c+di)} . Using Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^2 = -1} , we can rewrite this product in a form which clearly shows it to be another complex number:

$(a+bi)(c+di)=ac+adi+bci+bdi^{2}=(ac-bd)+(bc+ad)i.\$

To handle division, we simply note that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (c + di)(c - di) = c^2 +d^2} , so, provided that c and d are not simulateously zero,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{c + di} = \frac{c - di}{c^2 + d^2}, }

from which it follows that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{a + bi}{c + di} = \frac{(ac + bd) + (bc - ad)i}{c^2 + d^2}.}

If c = d = 0 then division by c+di is not defined.

Going a bit further, we can introduce the important operation of complex conjugation. Given an arbitrary complex number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = x + iy} , we define its complex conjugate to be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \bar{z} = x - iy} . Using the identity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a + b)(a - b) = a^2 - b^2} we derive the important formula

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z \bar{z} = x^2 + y^2}

and we define the modulus of a complex number z to be

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |z| = \sqrt{z \bar{z}}}

Note that the modulus of a complex number is always a nonnegative real number. The modulus (also called absolute value) satisfies three important properties that are completely analogous to the properties of the absolute value of real numbers

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |z| \ge 0} ; furthermore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |z| = 0} if and only if $z=0$
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |z_1 z_2| = |z_1| |z_2| \ }
• $|z_{1}+z_{2}|\leq |z_{1}|+|z_{2}|$

The last inequality is known as the triangle inequality.

The complex exponential

Recall that in real analysis, the ordinary exponential function may be defined as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots}

The same series may be used to define the complex exponential function

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^z = 1 + z + \frac{z^2}{2!} + \frac{z^3}{3!} + \cdots}

(where, of course, convergence is defined in terms of the complex modulus, instead of the real absolute value).

The complex exponential has the same multiplicative property that holds for real numbers, namely

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{z_1 + z_2} = e^{z_1} e^{z_2} \ }

The complex exponential function has the important property that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i\theta} = \cos \theta + i \sin \theta \ }

as may be seen immediately by substituting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = i\theta} and comparing terms with the usual power series expansions of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin \theta} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos \theta} .

The familiar trigonometric identity

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin^2 \theta + \cos^2 \theta = 1 \ }

immediately implies the important formula

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |e^{i\theta}| = 1} , for any Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta \in \mathbb{R}.}

Another way to establish this identity is to note that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \overline{e^{i\theta}} = e^{-i\theta}} , so

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |e^{i\theta}|^2 = e^{i\theta}e^{-i\theta} = e^0 = 1. \ }

Geometric interpretation

Graphical representation of a complex number and its conjugate

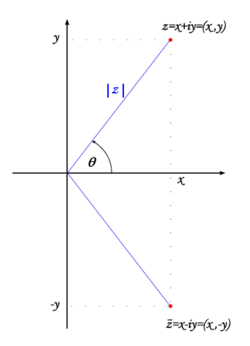
Since a complex number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = x + iy} is specified by two real numbers, namely Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} , it can be interpreted as the point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x,y)} in the plane. When complex numbers are represented as points in the plane, the resulting diagrams are known as Argand diagrams, after Robert Argand. The geometric representation of complex numbers turns out to be very useful, both as an aid to understanding the properties of complex numbers and as a tool in applying complex numbers to geometrical and physical problems.

There are no real surprises when we look at addition and subtraction in isolation: addition of complex numbers is not essentially different from addition of vectors in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \mathbb{R}^2} . Similarly, if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \alpha \in \mathbb{R}} is real, multiplication by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} is just scalar multiplication. In Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \mathbb{C}} we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_1 + z_2 = (x_1 + iy_1) + (x_2 + iy_2) = (x_1 + x_2) + i(y_1 + y_2) \ }

and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha z = \alpha(x + iy) = \alpha x + i\alpha y. \, }

To put it succintly, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \mathbb{C}} is a 2-dimensional real vector space with respect to the usual operations of addition of complex numbers and multiplication by a real number. There doesn't seem to be much more to say. But there is more to say, and that is that the multiplication of complex numbers has geometric significance. This is most easily seen if we take advantage of the complex exponential, and write complex numbers in polar form

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = r e^{i\theta}.}

Here, r is simply the modulus Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle |z| = \sqrt{x^2 + y^2}} or vector length. The number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} is just the angle formed with the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} -axis, and is called the argument. Now, when complex numbers are written in polar form, multiplication is very interesting

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_1 z_2 = (r_1 e^{i\theta_1}) (r_2 e^{i\theta_2}) = r_1 r_2 e^{i(\theta_1 + \theta_2)}.}

Multiplication by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} amounts to rotation by 90 degrees

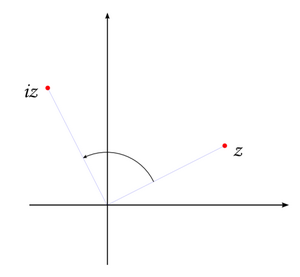
In other words, multiplication by a complex number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} has the effect of simultaneously scaling by the number's modulus and rotating by its argument. This is really astounding. For example, to multiply a given complex number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} we need only to rotate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi/2} (that is, 90 degrees). Translation corresponds to complex addition, scaling to multiplication by a real number, and rotation to multiplication by a complex number of unit modulus. The one type of coordinate transformation that is missing from this list is reflection. On the other hand, there is an arithmetic operation we have not considered, and that is division. Recall that for non-zero Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{z} = \frac{\bar{z}}{|z|^2}.}

Division of a complex number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_1} by a non-zero complex number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_2} can then be interpreted as multiplication of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_1} by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{z_2}} . This in turn corresponds to scaling of the modulus of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_1} by the inverse of the modulus of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_2} and a rotation of its argument by the negative of the argument of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_2} . That is,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{z_1}{z_2}=z_1 (\frac{1}{z_2})=\frac{1}{|z_2|^2}z_1 \overline{z_2}=\frac{|z_1|}{|z_2|}e^{i(\theta_1-\theta_2)},}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_1,\theta_2} are the arguments of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_1,z_2} , respectively.

Returning to the representation of complex numbers in rectangular form, we note that complex conjugation is just the transformation (or map) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle x + iy \;\mapsto\; x - iy} or, in vector notation, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle (x, y)\; \mapsto \;(x, -y)} . This is nothing other than reflection in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} -axis, and any other reflection may be obtained by combining that transformation with rotations and translations.

Historically, this observation was very important and led to the search for higher dimensional algebras that could "arithmetize" Euclidean geometry. It turns out that there are such generalizations in dimensions 4 and 8, known as the quaternions and octonions (also known as Cayley numbers). At that point, the process stops, but the ideas developed in this process have played an important role in the development of modern differential geometry and mathematical physics).

Algebraic closure

An important property of the set of complex numbers is that it is algebraically closed. This means that any non-constant polynomial with complex coefficients has a complex root. This result is known as the Fundamental Theorem of Algebra.

This is actually quite remarkable. We started out with the real numbers. There are many polynomials with real coefficients that do not have a real root. We took just one of these, the polynomial Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2+1} , and we introduced a new number, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} , which is defined to be a root of the polynomial. Suddenly, all non-constant polynomials have a root in this new setting where we allow complex numbers.

There are many proofs of the Fundamental Theorem of Algebra. Many of the simplest depend crucially on complex analysis. But it is by no means necessary to rely on complex analysis here. A proof using field theory is alluded to at the very end of this article.

Complex numbers in physics

Complex numbers appear everywhere in mathematical physics, but one area where the role of complex numbers is especially difficult to ignore is in quantum mechanics. There are a number of ways of formulating the basic laws of quantum mechanics, but here we consider just one: the Schrödinger equation, discovered by Erwin Schrödinger in 1926. In rectangular coordinates, it may be written

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar \frac{\partial \psi}{\partial t} = - \frac{\hbar^2}{2m}\Delta\psi + V(x,y,z)\psi,}

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}}

is known as the Laplacian operator and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x,y,z)} is the potential function. Now, there is some subtlety in the interpretation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} because a system can be affected by observation, and the functions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} we "see" must be eigenstates of the operator defined by the Schrödinger equation, but when we do measure, say, the position of a particle, the probability of finding it in a small region Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} is just

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_R\nolimits |\psi|^2. }

Formal definition

We have been treating complex numbers very much like real numbers and found that they can be very useful, but we have not yet proven that they exist or that they can be used without running into contradictions. In fact, it is quite easy to go wrong when using complex numbers. Consider for instance the following computation:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1=\sqrt{-1}\times\sqrt{-1}=\sqrt{(-1)\times(-1)}=\sqrt{1}=1.}

This computation seems to show that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1} equals Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} , which is nonsense. The point is that the second equality can not be applied. Positive real numbers satisfy the identity

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{a}\times\sqrt{b} = \sqrt{a \times b}, }

but this identity does not hold for negative real numbers, whose square roots are not real, because the square root symbol denotes only the positive solution to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2 = a} .

One possibility to feel more secure when using complex numbers is to define them in terms of constructs which are better understood. This approach was taken by Hamilton, who defined complex numbers as ordered pairs of real numbers, that is,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{C}= \{ (a,b) \colon a,b\in \mathbb{R} \}.}

Addition and multiplication of such pairs can be defined as follows:

• addition: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a, b) + (c, d) = (a + c, b + d)}
• multiplication: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a, b)(c, d) = (ac - bd, bc + ad)}

The multiplication may look artificial, but it is inspired by the formula

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a + bi)(c + di) = (ac - bd) + (bc + ad)i. \ }

which we derived before.

These definitions satisfy most of the basic properties of addition and multiplication of real numbers, and we can employ many formulas from the elementary algebra we are accustomed to. More specifically, it can easily be shown that addition and multiplication as defined above are commutative and associative, and that multiplication is distributive over addition; in other words, the sum (or the product) of two numbers does not depend on the order of terms; the sum (product) of three or more elements does not depend on order of operations ('we can suppress the parentheses'); the product of a complex number with a sum of two other numbers expands in the usual way. In mathematical language this means that with addition and multiplication defined this way, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{C}} satisfies the axioms for a field and is called the field of complex numbers.

Now we are ready to understand the 'real' meaning of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} . Observe that the pairs of type (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} ,0) are identical to the set of reals, so we write Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a,0)=a} . Observe also that by definition Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (0,1)(0,1) = (-1,0)=-1} . In other words, we can define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} , the symbol we've been using, as the pair (0,1). In this way we have a way of indicating which one we mean of the two solutions of the equation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^2=-1} ; the other is now denoted (0,-1).

Another way to define the complex numbers comes from field theory. Because Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2+1} is irreducible in the polynomial ring Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}[x]} , the ideal generated by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2+1} is a maximal ideal. Therefore, the quotient ring Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{C}=\mathbb{R}[x]/\left(x^2+1\right)} is a field. We can choose the polynomials of degree at most 1 as the representatives for the equivalence classes in this quotient ring. So in a sense, we can imagine that the dummy variable Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is the imaginary number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} , and the elements of the quotient ring behave exactly the way we expect the complex numbers to behave. For example, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2} is in the same equivalence class as $-1$, and so $x^{2}=-1$ in this quotient ring. (As a final comment in this analysis, we could next show that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{C}} has no finite extension and must therefore be algebraically closed.)