Maps of tetration: Difference between revisions
imported>Dmitrii Kouznetsov |
imported>Dmitrii Kouznetsov (add figure from the book) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[File:Tetreal10bx10d.png|400px|thumb|<math>y\!=\!\mathrm{tet}_b(x)</math> versus <math>x</math> for various <math>b</math> by | |||
<ref name="book"> | |||
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 <br> | |||
http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf <br> | |||
http://mizugadro.mydns.jp/BOOK/202.pdf | |||
Д.Кузнецов. Суперфункции. [[Lambert Academic Publishing]], 2014. | |||
</ref>]] | |||
[[File:Ack3a600.jpg|400px|thumb|Base <math>b=\sqrt{2}\approx 1.41</math>]] | [[File:Ack3a600.jpg|400px|thumb|Base <math>b=\sqrt{2}\approx 1.41</math>]] | ||
[[File:Ack3b600.jpg|400px|thumb|Henryk base, <math>b=\exp(1/\mathrm e)\approx 1.44</math>]] | [[File:Ack3b600.jpg|400px|thumb|Henryk base, <math>b=\exp(1/\mathrm e)\approx 1.44</math>]] | ||
| Line 6: | Line 13: | ||
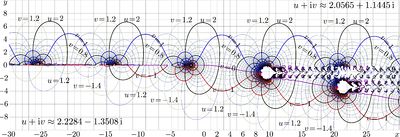
[[File:Ack4c.jpg|400px|thumb|Sheldon base, <math>b=1.52598338517+0.0178411853321 \,\mathrm i</math>]] | [[File:Ack4c.jpg|400px|thumb|Sheldon base, <math>b=1.52598338517+0.0178411853321 \,\mathrm i</math>]] | ||
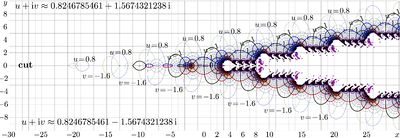
Article [[Maps of tetration]] collects some [[complex map]]s of [[tetration]] <math>\mathrm{tet}_b</math> to different values of base <math>b</math>. | Article [[Maps of tetration]] collects some [[complex map]]s of [[tetration]] <math>\mathrm{tet}_b</math> to different values of base <math>b</math>. | ||
For several real values of base <math>b\!>\!1</math> the real-real plots <math>y\!=\!\mathrm{tet}_b(x)</math> is shown at the upper figure at right. | |||
The [[complex map]]s correspond to the following values of base: | |||
<math>b=\sqrt{2} \approx 1.41</math>, | <math>b=\sqrt{2} \approx 1.41</math>, | ||
<math>b=\exp(1/\mathrm e) \approx 1.44</math>, | <math>b=\exp(1/\mathrm e) \approx 1.44</math>, | ||
| Line 73: | Line 83: | ||
==Book== | ==Book== | ||
The maps are plotted using the [[conto.cin]] code in [[C++]]. The [[Latex]] code is used to add the labels. | The maps are plotted using the [[conto.cin]] code in [[C++]]. The [[Latex]] code is used to add the labels. | ||
All the maps at right are supplied with generators; the colleagues may download the | All the maps at right are supplied with generators; the colleagues may download the codes and reproduce (or even modify) them. | ||
If some generator does not work as expected, let me know and let us correct it. | If some generator does not work as expected, let me know and let us correct it. | ||
The algorithms, used to evaluate the tetration to various bases, are described also in the [[Book]] | The algorithms, used to evaluate the tetration to various bases, are described also in the [[Book]] | ||
[[Суперфункции]], in Russian | [[Суперфункции]], in Russian | ||
<ref> | <ref name="book"> | ||
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 <br> | https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 <br> | ||
http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf <br> | http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf <br> | ||
Latest revision as of 04:34, 2 September 2014
Article Maps of tetration collects some complex maps of tetration Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{tet}_b} to different values of base Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} .
For several real values of base Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b\!>\!1} the real-real plots Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y\!=\!\mathrm{tet}_b(x)} is shown at the upper figure at right.
The complex maps correspond to the following values of base:
, , , , ,
Tetration is shown with lines of constant real part and lines of constant imaginary part ;
For this case, the regular iteration at fixed point is used. The evaluation is described in the Mathematics of Computation [2].
For , the exotic iteration at fixed point is used. The evaluation is described in the Mathematics of Computation [3].
For , the Cauchi integral is used for evaluation. It is described in Mathematics of Computation [4].
Historically, evaluation for the case was first to be reported. Namely for this case, the special algorithm fsexp.cin is loaded; it is described in Vladikavkaz Mathematical Jorunal [5].
Sheldon base
Tetration to Sheldon base is considered by the special request from Sheldon Levenstein. For this base, it was believed to be especially difficult to evaluate.
The evaluation uses almost the same algorithm of the Cauchi integral [4].
The small modification had been applied to the original algorithm; the condition is suppressed at the numerical solving of the corresponding integral equation for values of superfunction along . No difficulties, specific namely for this complex value of base , had been detected.
Book
The maps are plotted using the conto.cin code in C++. The Latex code is used to add the labels. All the maps at right are supplied with generators; the colleagues may download the codes and reproduce (or even modify) them. If some generator does not work as expected, let me know and let us correct it.
The algorithms, used to evaluate the tetration to various bases, are described also in the Book Суперфункции, in Russian [1]. For year 2014, the English version is not yet ready. The images above are prepared for the article "Holomorphic ackermanns" [6].
Content of the first version of this article is adopted from TORI, http://mizugadro.mydns.jp/t/index.php/Maps_of_tetration
References
- ↑ 1.0 1.1
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf
http://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014. - ↑
http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
http://www.ils.uec.ac.jp/~dima/PAPERS/2010q2.pdf
http://mizugadro.mydns.jp/PAPERS/2010q2.pdf D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756. - ↑
http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf
http://mizugadro.mydns.jp/PAPERS/2012e1eMcom2590.pdf
http://mizugadro.mydns.jp/PAPERS/2011e1e.pdf H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). Mathematics of Computation. Math. Comp., v.81 (2012), p. 2207-2227. ISSN 1088-6842(e) ISSN 0025-5718(p) - ↑ 4.0 4.1
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf
http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670. - ↑ http://mizugadro.mydns.jp/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.
- ↑ D.Kouznetsov. Holomorphic ackermanns. 2015, in preparation.