Vapor pressure: Difference between revisions
imported>Milton Beychok (Expanded the section on vapor pressure of solids. Also relocated that section.) |
mNo edit summary |
||
| (21 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
'''Vapor pressure''' (also known as ''equilibrium vapor pressure''), is the [[pressure]] of a [[vapor]] in [[Thermodynamic equilibrium|equilibrium]] with its [[liquid]] or [[solid]] [[Phase (matter)|phase]].<ref name=Jesperson>{{cite book|author=Neil D. Jesperson|title=Chemistry|edition= |publisher=Barron's Educational Series|year=1997|id=ISBN 0-8120-9503-0}}</ref><ref name=Mortimer>{{cite book|author=Robert G. Mortimer|title=Physical Chemistry|edition=3rd Edition|publisher=Academic Press|year=2008|id=ISBN 0-12-370617-3}}</ref> At any given [[temperature]], for a specific substance, there is a [[pressure]] at which the gas of that specific substance is in | '''Vapor pressure''' (also known as ''equilibrium vapor pressure''), is the [[pressure]] of a [[vapor]] in [[Thermodynamic equilibrium|equilibrium]] with its [[liquid]] or [[solid]] [[Phase (matter)|phase]].<ref name=Jesperson>{{cite book|author=Neil D. Jesperson|title=Chemistry|edition= |publisher=Barron's Educational Series|year=1997|id=ISBN 0-8120-9503-0}}</ref><ref name=Mortimer>{{cite book|author=Robert G. Mortimer|title=Physical Chemistry|edition=3rd Edition|publisher=Academic Press|year=2008|id=ISBN 0-12-370617-3}}</ref> At any given [[temperature]], for a specific substance, there is a [[pressure]] at which the gas of that specific substance is in equilibrium with its liquid or solid forms — i.e., when the rates at which molecules escape from and return into the vaporizing liquid or solid are equal. This is the vapor pressure of the specific substance at that temperature. | ||
The vapor pressure of a substance increases with increasing temperature. | The vapor pressure of a substance increases with increasing temperature. | ||
==Volatility of liquids== | ==Volatility of liquids== | ||
| Line 15: | Line 15: | ||
{{main|Antoine equation}} | {{main|Antoine equation}} | ||
The Antoine equation <ref>[http://antoine.frostburg.edu/chem/senese/101/liquids/faq/antoine-vapor-pressure.shtml What is the Antoine Equation?] (Chemistry Department, [[Frostburg State University]], [[Maryland]])</ref><ref>{{cite book|author=R.K.Sinnot|title=Chemical Engineering Design|edition=4th Edition|publisher=Butterworth-Heinemann|year=2005|id=ISBN 0-7506-6538-6}}</ref> is a mathematical expression of the relation between the vapor pressure and the temperature of pure substances. The basic form of the equation is: | The Antoine equation <ref name=frostburg>[http://antoine.frostburg.edu/chem/senese/101/liquids/faq/antoine-vapor-pressure.shtml What is the Antoine Equation?] (Chemistry Department, [[Frostburg State University]], [[Maryland (U.S. state)|Maryland]])</ref><ref>{{cite book|author=R.K.Sinnot|title=Chemical Engineering Design|edition=4th Edition|publisher=Butterworth-Heinemann|year=2005|id=ISBN 0-7506-6538-6}}</ref> is a mathematical expression of the relation between the vapor pressure and the temperature of pure liquid or solid substances. The basic form of the equation is: | ||
:<math>\log P = A-\frac{B}{C+T}</math> | :<math>\log P = A-\frac{B}{C+T}</math> | ||
| Line 35: | Line 35: | ||
:<math>T = \frac{B}{A-\log P}</math> | :<math>T = \frac{B}{A-\log P}</math> | ||
Sublimations and vaporizations of the same substance have separate sets of Antoine coefficients, as do components in mixtures.<ref name=frostburg/> The Antoine equation is accurate to a few percent for most volatile substances (with vapor pressures over 10 Torr). | |||
==Vapor pressures and normal boiling points of liquids == | ==Vapor pressures and normal boiling points of liquids == | ||
{{main|Boiling point}} | {{main|Boiling point}} | ||
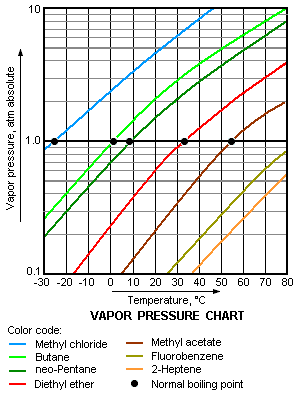
{{Image|Vapor Pressure Chart2.png|right|350px|A typical vapor pressure graph of various liquids.}} | |||
The [[atmospheric pressure]] boiling point of a liquid (also known as the [[normal boiling point]]) is the temperature where the vapor pressure equals the ambient atmospheric pressure. With any incremental increase in that temperature, the vapor pressure becomes sufficient to overcome atmospheric pressure and lift the liquid to form bubbles inside the bulk of the substance. Bubble formation deeper in the liquid requires a higher pressure, and therefore higher temperature, because the fluid pressure | The [[atmospheric pressure]] boiling point of a liquid (also known as the [[normal boiling point]]) is the temperature where the vapor pressure equals the ambient atmospheric pressure. With any incremental increase in that temperature, the vapor pressure becomes sufficient to overcome atmospheric pressure and lift the liquid to form bubbles inside the bulk of the substance. Bubble formation deeper in the liquid requires a higher pressure, and therefore higher temperature, because the fluid pressure becomes higher than atmospheric pressure as the depth increases. | ||
The higher the vapor pressure of a liquid at a given temperature, the lower the normal boiling point (i.e., the boiling point at atmospheric pressure) of the liquid. | The higher the vapor pressure of a liquid at a given temperature, the lower the normal boiling point (i.e., the boiling point at atmospheric pressure) of the liquid. | ||
| Line 46: | Line 48: | ||
The vapor pressure chart to the right has graphs of the vapor pressures versus temperatures for a variety of liquids.<ref name=Perry/> As can be seen in the chart, the liquids with the highest vapor pressures have the lowest normal boiling points. | The vapor pressure chart to the right has graphs of the vapor pressures versus temperatures for a variety of liquids.<ref name=Perry/> As can be seen in the chart, the liquids with the highest vapor pressures have the lowest normal boiling points. | ||
For example, at any given temperature, [[ | For example, at any given temperature, [[methyl chloride]] has the highest vapor pressure of any of the liquids in the chart. It also has the lowest normal boiling point (– 26 °C), which is where the vapor pressure curve of methyl chloride (the blue line) intersects the horizontal pressure line of one atmosphere ([[Atmosphere (unit)|atm]]) of absolute vapor pressure. | ||
As another example, butane has a vapor pressure of 1 atmosphere at about 0 degrees Celsius. As a result, at sea level the temperature must be higher than this in order for a butane lighter to function, since the pressure of the butane vapor must be above 1 atmosphere in order for the vapor to escape from its container into the surrounding air. | |||
Although the relation between vapor pressure and temperature is non-linear, the chart uses a logarithmic vertical axis in order to obtain slightly curved lines so that one chart can graph many liquids. | Although the relation between vapor pressure and temperature is non-linear, the chart uses a logarithmic vertical axis in order to obtain slightly curved lines so that one chart can graph many liquids. | ||
| Line 54: | Line 58: | ||
{{main|Pressure}} | {{main|Pressure}} | ||
The international [[SI]] unit for pressure is the [[pascal (unit)|pascal]] (Pa), equal to one [[newton]] per [[square meter]] (N·m<sup>-2</sup> or kg·m<sup>-1</sup>·s<sup>-2</sup>). The conversions to other pressure units are: | The international [[SI]] unit for pressure is the [[pascal (unit)|pascal]] (Pa), equal to one [[newton]] per [[square meter]] (N·m<sup>-2</sup> or kg·m<sup>-1</sup>·s<sup>-2</sup>). The conversions to other pressure units are: | ||
{{pressure}} | {{pressure}}<br/> | ||
'''About the torr:''' There is no consensus in the technical literature about whether the name of the torr should be "Torr" or "torr". Nor is there any consensus about whether the symbol for that unit of pressure should be "Torr" or "torr". Both the [[United Kingdom]]'s [[National Physical Laboratory]] (see [http://www.npl.co.uk/reference/faqs/pressure-units Pressure Units]) and [[New Zealand]]'s [[Measurement Standards Laboratory]] (see [http://msl.irl.cri.nz/sites/all/files/training-manuals/TG19-July-2009.pdf Barometric Pressure Units]) use "torr" as the name and as the symbol. An extensive search of the website of the [[United States of America|U.S.]] [[National Institute of Standards and Technology]] found no such clear-cut definitions. Therefore, this table uses "torr" as both the name and the symbol. | |||
==Vapor pressure of liquid mixtures== | ==Vapor pressure of liquid mixtures== | ||
| Line 61: | Line 66: | ||
Raoult's law gives an approximation to the vapor pressure of mixtures of liquids.<ref name=Jesperson/><ref name=Mortimer/> It states that the vapor pressure of a liquid mixture is equal to the mole-fraction-weighted sum of the vapor pressures of the mixture's pure components: | Raoult's law gives an approximation to the vapor pressure of mixtures of liquids.<ref name=Jesperson/><ref name=Mortimer/> It states that the vapor pressure of a liquid mixture is equal to the mole-fraction-weighted sum of the vapor pressures of the mixture's pure components: | ||
:<math> | :<math> p_\text{tot} = \sum_i p_i \chi_i \,</math> | ||
where '''''p'''''<sub> '''tot'''</sub> is the mixture's vapor pressure, '''''i''''' is one of the components of the mixture and '''''Χ<sub>i</sub>''''' is the [[mole fraction]] of that component in the liquid mixture. The term '''''p<sub>i</sub>Χ<sub>i</sub>''''' is the partial pressure of component '''''i''''' in the mixture. | |||
Raoult's law is applicable only to ideal liquids and to components that are fairly similar such as [[benzene]] and [[toluene]], [[hexane and heptane]] or [[o-xylene]] and [[p-xylene]]. | Raoult's law is applicable only to ideal liquids and to components that are fairly similar such as [[benzene]] and [[toluene]], [[hexane and heptane]] or [[o-xylene]] and [[p-xylene]]. | ||
| Line 87: | Line 77: | ||
==Vapor pressure of solids== | ==Vapor pressure of solids== | ||
{{Image|Vapor Pressure of Liquid and Solid Benzene.png|right|350px|Vapor pressure of liquid and solid [[benzene]]}} | |||
All solid materials have a vapor pressure which, for most solids, is very low. Some notable exceptions are [[naphthalene]], [[ice]] and [[dry ice]] ([[carbon dioxide]]). The vapor pressure of dry ice is 5.73 MPa (56.5 atm) at 20 °C which would cause most sealed containers to rupture. | All solid materials have a vapor pressure which, for most solids, is very low. Some notable exceptions are [[naphthalene]], [[ice]] and [[dry ice]] ([[carbon dioxide]]). The vapor pressure of dry ice is 5.73 MPa (56.5 atm) at 20 °C which would cause most sealed containers to rupture. | ||
| Line 95: | Line 85: | ||
The vapor pressure of a solid can be defined as the pressure at which the rate of [[sublimation (physics)|sublimation]] of a solid matches the rate of deposition of its vapor phase. | The vapor pressure of a solid can be defined as the pressure at which the rate of [[sublimation (physics)|sublimation]] of a solid matches the rate of deposition of its vapor phase. | ||
There are a number of methods for calculating the sublimation pressure (i.e., the vapor pressure) of a solid. One method is to | There are a number of methods for calculating the sublimation pressure (i.e., the vapor pressure) of a solid. One method is to estimate the sublimation pressure from extrapolated liquid vapor pressures (of the supercooled liquid), if the [[Enthalpy of fusion|heat of fusion]] is known, by using this particular form of the [[Clausius–Clapeyron relation]]:<ref>Moller B., Rarey J., Ramjugernath D., "Estimation of the vapour pressure of non-electrolyte organic compounds via group contributions and group interactions ", J.Mol.Liq., 143(1), 52-63, 2008</ref> | ||
:<math>\log\,P^S_\mathrm {solid} = \log\,P^S_\mathrm{liquid} - \frac{\Delta H_m}{R} \left( \frac{1}{T} - \frac{1}{T_m} \right)</math> | :<math>\log\,P^S_\mathrm {solid} = \log\,P^S_\mathrm{liquid} - \frac{\Delta H_m}{R} \left( \frac{1}{T} - \frac{1}{T_m} \right)</math> | ||
| Line 122: | Line 112: | ||
|} | |} | ||
gives a fair estimation for temperatures not too far from the melting point. | This method assumes that the heat of fusion is temperature-independent, ignores additional transition temperatures between different solid phases, and it gives a fair estimation for temperatures not too far from the melting point. It also shows that the sublimation pressure is lower than the extrapolated liquid vapor pressure (Δ''H''<sub>m</sub> is positive) and the difference grows with increased distance from the melting point. | ||
==Relative humidity== | ==Relative humidity== | ||
{{main|Relative humidity}} | {{main|Relative humidity}} | ||
The ratio, often expressed as a percentage, of the partial pressure of water in the atmosphere at some observed temperature, to the vapor pressure of pure water at this temperature.<ref>[http:// | The ratio, often expressed as a percentage, of the partial pressure of water in the atmosphere at some observed temperature, to the vapor pressure of pure water at this temperature.<ref>[http://goldbook.iupac.org/R05267.html Relative Humidity] [[IUPAC]] Compendium of Chemical Terminology (Electronic version)</ref> It may be expressed as: | ||
:<math>% RH = \Big(\frac{p_\mathrm{water}}{P^o_\mathrm{water}}\Big) 100</math> | :<math>% RH = \Big(\frac{p_\mathrm{water}}{P^o_\mathrm{water}}\Big) 100</math> | ||
| Line 163: | Line 153: | ||
==References== | ==References== | ||
{{reflist}} | |||
[[Category:Suggestion Bot Tag]] | |||
Latest revision as of 12:00, 4 November 2024
Vapor pressure (also known as equilibrium vapor pressure), is the pressure of a vapor in equilibrium with its liquid or solid phase.[1][2] At any given temperature, for a specific substance, there is a pressure at which the gas of that specific substance is in equilibrium with its liquid or solid forms — i.e., when the rates at which molecules escape from and return into the vaporizing liquid or solid are equal. This is the vapor pressure of the specific substance at that temperature.
The vapor pressure of a substance increases with increasing temperature.
Volatility of liquids
The vapor pressure is an indication of a liquid's evaporation rate. It relates to the tendency of molecules and atoms to escape from a liquid or a solid. A substance with a high vapor pressure at normal temperatures is often referred to as volatile.
Relative volatility is a measure that compares the vapor pressures of the components in a liquid mixture of chemicals. This measure is widely used in designing large industrial distillation, absorption and other separation processes that involve the contacting of vapor and liquid phases in a series of equilibrium stages.[3][4][5] In effect, it indicates the ease or difficulty of separating the more volatile components from the less volatile components in a liquid mixture.
Calculating vapor pressures with Antoine equation
The Antoine equation [6][7] is a mathematical expression of the relation between the vapor pressure and the temperature of pure liquid or solid substances. The basic form of the equation is:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \log P = A-\frac{B}{C+T}}
and it can be transformed into this temperature-explicit form:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = \frac{B}{A-\log P} - C}
where: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P}
is the absolute vapor pressure of a substance
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T}
is the temperature of the substance
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A}
, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B}
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C}
are substance-specific coefficients (i.e., constants or parameters)
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \log} is typically either Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \log_{10}} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \log_e}
A simpler form of the equation with only two coefficients is sometimes used:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \log P = A-\frac{B}{T}}
which can be transformed to:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = \frac{B}{A-\log P}}
Sublimations and vaporizations of the same substance have separate sets of Antoine coefficients, as do components in mixtures.[6] The Antoine equation is accurate to a few percent for most volatile substances (with vapor pressures over 10 Torr).
Vapor pressures and normal boiling points of liquids
The atmospheric pressure boiling point of a liquid (also known as the normal boiling point) is the temperature where the vapor pressure equals the ambient atmospheric pressure. With any incremental increase in that temperature, the vapor pressure becomes sufficient to overcome atmospheric pressure and lift the liquid to form bubbles inside the bulk of the substance. Bubble formation deeper in the liquid requires a higher pressure, and therefore higher temperature, because the fluid pressure becomes higher than atmospheric pressure as the depth increases.
The higher the vapor pressure of a liquid at a given temperature, the lower the normal boiling point (i.e., the boiling point at atmospheric pressure) of the liquid.
The vapor pressure chart to the right has graphs of the vapor pressures versus temperatures for a variety of liquids.[4] As can be seen in the chart, the liquids with the highest vapor pressures have the lowest normal boiling points.
For example, at any given temperature, methyl chloride has the highest vapor pressure of any of the liquids in the chart. It also has the lowest normal boiling point (– 26 °C), which is where the vapor pressure curve of methyl chloride (the blue line) intersects the horizontal pressure line of one atmosphere (atm) of absolute vapor pressure.
As another example, butane has a vapor pressure of 1 atmosphere at about 0 degrees Celsius. As a result, at sea level the temperature must be higher than this in order for a butane lighter to function, since the pressure of the butane vapor must be above 1 atmosphere in order for the vapor to escape from its container into the surrounding air.
Although the relation between vapor pressure and temperature is non-linear, the chart uses a logarithmic vertical axis in order to obtain slightly curved lines so that one chart can graph many liquids.
Units of vapor pressure
The international SI unit for pressure is the pascal (Pa), equal to one newton per square meter (N·m-2 or kg·m-1·s-2). The conversions to other pressure units are:
| pascal (Pa) |
bar (bar) |
atmosphere (atm) |
torr (torr) |
pound-force per square inch (psi) |
kilogram-force per square centimeter (kgf/cm2) | |
|---|---|---|---|---|---|---|
| 1 Pa | ≡ 1 N/m2 | 10−5 | 9.8692×10−6 | 7.5006×10−3 | 145.04×10−6 | 1.01972×10−5 |
| 1 bar | 100,000 | ≡ 106 dyn/cm2 | 0.98692 | 750.06 | 14.504 | 1.01972 |
| 1 atm | 101,325 | 1.01325 | ≡ 1 atm | 760 | 14.696 | 1.03323 |
| 1 torr | 133.322 | 1.3332×10−3 | 1.3158×10−3 | ≡ 1 torr ≈ 1 mmHg |
19.337×10−3 | 1.35951×10−3 |
| 1 psi | 6,894.76 | 68.948×10−3 | 68.046×10−3 | 51.715 | ≡ 1 lbf/in2 | 7.03059×10−2 |
| 1 kgf/cm2 | 98,066.5 | 0.980665 | 0.967838 | 735.5576 | 14.22357 | ≡ 1 kgf/cm2 |
Example reading: 1 Pa = 1 N/m2 = 10−5 bar = 9.8692×10−6 atm = 7.5006×10−3 torr, etc.
Note: mmHg is an abbreviation for millimetre of mercury
About the torr: There is no consensus in the technical literature about whether the name of the torr should be "Torr" or "torr". Nor is there any consensus about whether the symbol for that unit of pressure should be "Torr" or "torr". Both the United Kingdom's National Physical Laboratory (see Pressure Units) and New Zealand's Measurement Standards Laboratory (see Barometric Pressure Units) use "torr" as the name and as the symbol. An extensive search of the website of the U.S. National Institute of Standards and Technology found no such clear-cut definitions. Therefore, this table uses "torr" as both the name and the symbol.
Vapor pressure of liquid mixtures
Raoult's law gives an approximation to the vapor pressure of mixtures of liquids.[1][2] It states that the vapor pressure of a liquid mixture is equal to the mole-fraction-weighted sum of the vapor pressures of the mixture's pure components:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_\text{tot} = \sum_i p_i \chi_i \,}
where p tot is the mixture's vapor pressure, i is one of the components of the mixture and Χi is the mole fraction of that component in the liquid mixture. The term piΧi is the partial pressure of component i in the mixture.
Raoult's law is applicable only to ideal liquids and to components that are fairly similar such as benzene and toluene, hexane and heptane or o-xylene and p-xylene.
Systems that have vapor pressures higher than indicated by the above equation are said to have positive deviations. Such a deviation suggests weaker intermolecular attraction than in the pure components, so that the molecules can be thought of as being "held in" the liquid phase less strongly than in the pure liquid. An example is the azeotrope of approximately 95% ethanol and water. Because the azeotrope's vapor pressure is higher than predicted by Raoult's law, it boils at a temperature below that of either pure component.
There are also systems with negative deviations that have vapor pressures that are lower than expected. Such a deviation is evidence for stronger intermolecular attraction between the constituents of the mixture than exists in the pure components. Thus, the molecules are "held in" the liquid more strongly when a second molecule is present. An example is a mixture of trichloromethane (chloroform) and 2-propanone (acetone), which boils above the boiling point of either pure component.
Vapor pressure of solids
All solid materials have a vapor pressure which, for most solids, is very low. Some notable exceptions are naphthalene, ice and dry ice (carbon dioxide). The vapor pressure of dry ice is 5.73 MPa (56.5 atm) at 20 °C which would cause most sealed containers to rupture.
Due to their often extremely low values, measurement of the vapor pressure of solids can be rather difficult. Typical techniques for such measurements include the use of thermogravimetry and gas transpiration.
The vapor pressure of a solid can be defined as the pressure at which the rate of sublimation of a solid matches the rate of deposition of its vapor phase.
There are a number of methods for calculating the sublimation pressure (i.e., the vapor pressure) of a solid. One method is to estimate the sublimation pressure from extrapolated liquid vapor pressures (of the supercooled liquid), if the heat of fusion is known, by using this particular form of the Clausius–Clapeyron relation:[8]
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \log\,P^S_\mathrm {solid} = \log\,P^S_\mathrm{liquid} - \frac{\Delta H_m}{R} \left( \frac{1}{T} - \frac{1}{T_m} \right)}
where: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P^S_\mathrm{solid}} = Sublimation pressure of the solid component at the temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T\!<T_m} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P^S_\mathrm{liquid}} = Extrapolated vapor pressure of the liquid component at the temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T\!<T_m} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta H_m} = Heat of fusion Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} = Universal gas constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} = Sublimation temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_m} = Melting point temperature
This method assumes that the heat of fusion is temperature-independent, ignores additional transition temperatures between different solid phases, and it gives a fair estimation for temperatures not too far from the melting point. It also shows that the sublimation pressure is lower than the extrapolated liquid vapor pressure (ΔHm is positive) and the difference grows with increased distance from the melting point.
Relative humidity
The ratio, often expressed as a percentage, of the partial pressure of water in the atmosphere at some observed temperature, to the vapor pressure of pure water at this temperature.[9] It may be expressed as:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle % RH = \Big(\frac{p_\mathrm{water}}{P^o_\mathrm{water}}\Big) 100}
| where: | |
| Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle % RH} | = percent relative humidity of the atmospheric air-water mixture |
| Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_\mathrm{water}} | = partial pressure of water in the atmospheric air-water mixture |
| Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P^o_\mathrm{water}} | = vapor pressure of pure water at the temperature of the atmospheric air-water mixture |
At 100 percent relative humidity, the atmospheric air is said to be saturated with water. That occurs when the partial pressure of the water in the air, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_\mathrm{water}} , is equal to the vapor pressure of pure water at the air temperature, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P^o_\mathrm{water}} .
Given the wet-bulb temperature and the dry-bulb temperature of the atmosphere, which are readily measured by using a sling psychrometer, the relative humidity can be obtained from a psychrometric chart.[4]
Vapor pressure terminology in meteorology
The terminology defined and discussed in this article is the terminology used extensively by chemists, chemical engineers and others.
The terminology used by workers in the field of meteorology is unique to that field of science and it defines vapor pressure and similar terms quite a bit differently than is done in this article. For example, the American Meteorological Society (AMS) uses the following definitions:[10]
- Vapor pressure: The portion of the total air pressure exerted by the water vapor component of air. (That would be the partial pressure of the water vapor in the air using the terminology defined in this article.)
- Saturation vapor pressure: The maximum vapor pressure in a sample of air at a specific temperature. (That is not the meaning of "saturation vapor pressure" as defined in this article. In the terminology defined in this article, it can be said that air at a specific temperature is saturated when the partial pressure of the water in the air is equal to the vapor pressure of pure water at that specific temperature. In other words, when relative humidity is 100%.)
To avoid any confusion, this article makes no attempt to go into any further detail concerning the terminology used in meteorology.
References
- ↑ 1.0 1.1 Neil D. Jesperson (1997). Chemistry. Barron's Educational Series. ISBN 0-8120-9503-0.
- ↑ 2.0 2.1 Robert G. Mortimer (2008). Physical Chemistry, 3rd Edition. Academic Press. ISBN 0-12-370617-3.
- ↑ Kister, Henry Z. (1992). Distillation Design, 1st Edition. McGraw-hill. ISBN 0-07-034909-6.
- ↑ 4.0 4.1 4.2 Perry, R.H. and Green, D.W. (Editors) (1984). Perry's Chemical Engineers' Handbook, 6th Edition. McGraw-hill. ISBN 0-07-049479-7.
- ↑ Seader, J. D., and Henley, Ernest J. (1998). Separation Process Principles. New York: Wiley. ISBN 0-471-58626-9.
- ↑ 6.0 6.1 What is the Antoine Equation? (Chemistry Department, Frostburg State University, Maryland)
- ↑ R.K.Sinnot (2005). Chemical Engineering Design, 4th Edition. Butterworth-Heinemann. ISBN 0-7506-6538-6.
- ↑ Moller B., Rarey J., Ramjugernath D., "Estimation of the vapour pressure of non-electrolyte organic compounds via group contributions and group interactions ", J.Mol.Liq., 143(1), 52-63, 2008
- ↑ Relative Humidity IUPAC Compendium of Chemical Terminology (Electronic version)
- ↑ AMS Glossary of Atmospheric Terms
- Pages using ISBN magic links
- Editable Main Articles with Citable Versions
- CZ Live
- Chemistry Workgroup
- Physics Workgroup
- Engineering Workgroup
- Chemical Engineering Subgroup
- Articles written in American English
- Advanced Articles written in American English
- All Content
- Chemistry Content
- Physics Content
- Engineering Content
- Chemical Engineering tag
- Pages with math errors
- Pages with math render errors